Intro
Leetcode 1498번 문제 Number of Subsequences That Satisfy the Given Sum Condition를 풀이하는데, 처음에는 Brute force로 풀다 안되어서 슬라이딩 윈도우 방식으로 시도를 해 보았습니다.
그런데 속도를 개선하고 보니 다른 문제가 있었습니다. 조건에 따르면 최대 2의 10000 제곱까지도 계산을 해야 하는데, 이 크기가 만만치 않습니다.
2의 1만제곱이 얼마나 큰지 long타입은 커녕 double로도 담을 수 없습니다. Double.MAX_VALUE 를 확인 해 보면

2의 1023 제곱까지는 담기는데, 1024제곱부터는 담기지 않습니다.
코드를 작성해서 확인 해보면 아래 보이는 것 처럼, 범위 밖의 숫자는 Infinity로 나옵니다.
System.err.println("Math.pow(2, 1023) = " + Math.pow(2, 1023));
System.err.println("Math.pow(2, 1024) = " + Math.pow(2, 1024));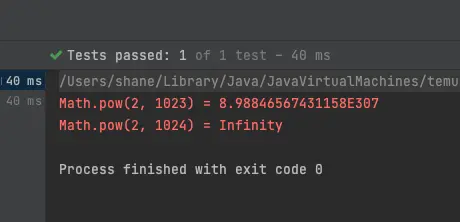
얼마나 큰 숫자일까요..? 2¹⁰⁰⁰⁰⁰ 은 이진수로는 10000 +1 자리로 표현이 될텐데요. 십진수로 표현한다면.. Math.log10(2) 의 결과가 0.30102 정도 되기 때문에, 거기 10만을 곱해서 대강 3만자리 이상이라는 계산이 나옵니다. 정말 어마어마하게 크죠.
MOD를 구하기 위해서는 값을 먼저 구해야 하는데 값을 구하는것 부터가 큰 난관인거죠.
이번 문제의 정의는 2의 10000승을 10⁹+7 로 나눈 나머지 구하기 로 하겠습니다.
왜 하필 leetcode의 대부분의 문제에서 MOD 값이 10⁹+7 인가 하면..
정확한 이유는 저도 모르지만 개인적으로는 2로 곱해도 Integer overflow가 되지 않으면서, 충분히 큰 Prime number라서 제법 괜찮은 수라고 봅니다.
해결하기
일단 테스트 코드를 아래와 같이 작성하고 구현체를 하나씩 만들어보며 해결해보겠습니다.
public class BinaryExponentiation {
@Test
void test() {
StopWatch stopWatch = new StopWatch();
Set<Integer> answers = new HashSet<>();
answers.add(measure(new IterateCalculator(), stopWatch));
// ...
Assertions.assertThat(answers).hasSize(1);
System.out.println("stopwach = " + stopWatch.prettyPrint());
}
private int measure(Calculator calculator, StopWatch stopWatch) {
final int BASE = 2;
final int POW = 10000;
final int MOD = (int) 1e9 + 7;
stopWatch.start(calculator.getClass().getSimpleName());
List<Integer> answers = new ArrayList<>();
for (int i = 0; i < 10000; i++) {
answers.add(calculator.calc(BASE, POW, MOD));
}
stopWatch.stop();
return answers.get(0);
}
interface Calculator {
int calc(int base, int pow, int mod);
}
// TODO: 구현체 객체들..
}보다 정확한 성능 테스트를 위해 각 연산은 1만번을 수행합니다. 해당 문제에서는 각 연산도 최대 10만번까지 필요하기때문에 연산속도가 중요합니다.
반복문
10000번을 곱하면서 매번 모듈러 연산을 하면 되겠네요. 10000이 그리 큰 숫자도 아니니깐 연산 1만번 쯤이야 껌이죠..?
바로 코드로 작성합니다.
class IterateCalculator implements Calculator {
@Override
public int calc(int base, int pow, int mod) {
long cur = 1L;
for (int i = 0; i < pow; i++) {
cur = (cur * base) % mod;
}
return (int) cur;
}
}코드도 직관적이고 간단합니다. 1만번 돌리는데 걸리는 시간을 측정 해 봅니다.
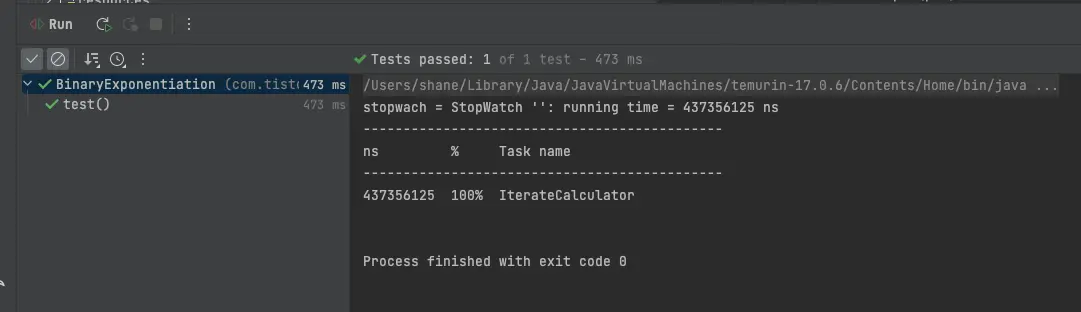
437 ms
0.4초 정도 걸린다고 하는데, 10만번이면 4초가넘게 걸리겠네요. TLE(Time Limit Exceeded)가 뜨게됩니다. 저도 처음엔 이렇게 해서 코드를 제출했다가 실패했습니다.
BigInteger
그러면.. 자바 코테의 치트키인 BigInteger 를 쓰면 되지 않을까? 그래서 한번 해봤습니다.
class BigIntegerCalculator implements Calculator {
@Override
public int calc(int base, int pow, int mod) {
return BigInteger.valueOf(base)
.pow(pow)
.mod(BigInteger.valueOf(mod))
.intValue();
}
}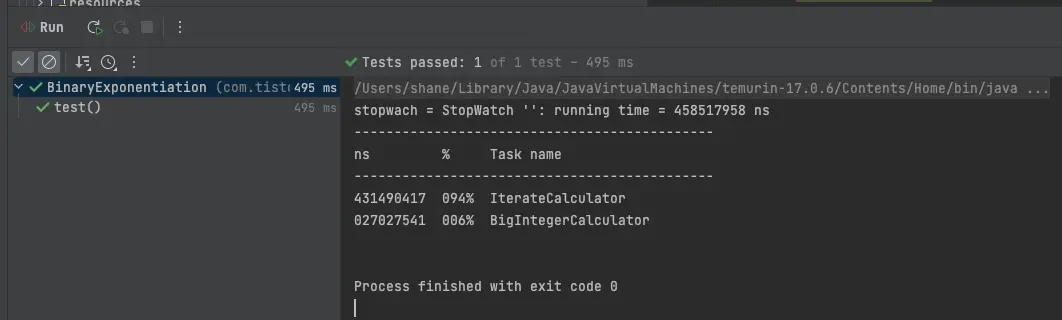
테스트도 통과 (값이 반복문 이용한 것과 같음) 했습니다. 역시 치트키 답습니다. 아무리 큰 숫자도 다 처리해줍니다.
하지만 문제가 있습니다. BigInteger가 아무리 큰 수의 연산도 매우 효율적으로 처리할 수 있도록 잘 구현되어 있다고 해도 위와 같은 계산을 한번만 하고 마는게 아니고 굉장히 많이 하려다 보니 한계가 있었습니다. 10만번에 0.3초라고 해도 느린건 느린겁니다.
일단 BigInteger 계산으로 leetcode 에서 제출을 했을때 어찌 통과는 되었지만
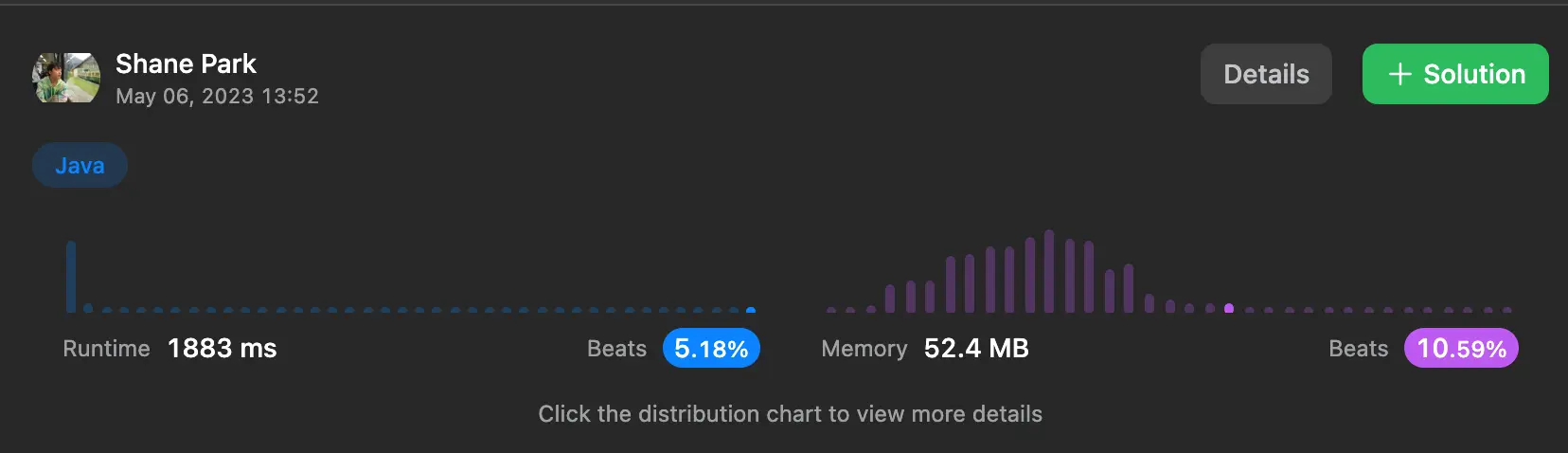
Runtime이 무려 1883 ms
위에 보이는 것 처럼 결론적으로 모든 테케 처리에 걸린 시간이 1883ms로 엄청나게 느렸습니다.
무엇보다도 BigInteger 사용이 금지된다면 무용지물인 방법 입니다. (실제 BigInteger 쓰지 말라고 하는 경우가 많음)
Binary Exponentiation
이번 글의 핵심입니다. Binary Exponentiation 혹은 Exponentiation by squaring 라고 합니다.
적절한 번역을 찾지는 못했는데 이진 거듭제곱이라고 부르면 어떨까요? 제곱을 분할 정복해서 효율을 높이는 방법입니다.
A¹³ 을 계산하는 경우를 예시로 들겠습니다.
A를 13번 곱한 값을 구하려면 일반적으로는 초기값을 1부터 시작했다고 봤을때 총 13번의 곱셈이 필요합니다. O(N)
그런데, A¹³ 을 A⁸ * A⁴ * A¹ 로 나누어 생각하면 어떨까요?
13을 이진수로 표현하면 1101이 됩니다. 각 자리수별로 1이 표시된 값을 곱해주면 원하는 값이 나옵니다. (셋째 자리수의 0이 계산에서 빠진 A² 를 의미함)
1부터 시작해서 A를 곱하고, 제곱해서 A² 를 계산하고, 또 제곱하여 A⁴를 계산하고, 그 다음에는 A⁴를 제곱해서 A⁸를 계산합니다.
겨우 4번의 계산만에 결과를 계산하는데 필요한 수를 다 만들어냈습니다. N 번의 연산이 Log(N)이 되는 기적이 일어난겁니다.
13정도야 우습지만, 그 숫자가 커질수록 차이가 급격히 벌어집니다. 우리 프로그래머들은 이진 들어간 친구들의 말도 안되는 뛰어난 성능을 익히 잘 알고 있기 때문에 더이상 언급은 않겠습니다.
이제 코드를 작성해 보겠습니다.
class BinaryExponentiationCalculator implements Calculator {
@Override
public int calc(int base, int pow, int mod) {
long result = 1;
for (; pow > 0; pow /= 2) {
if (pow % 2 == 1) {
result = (result * base) % mod;
}
base = (int) ((long) base * base % mod);
}
return (int) result;
}
}기본 아이디어는 기본값(base)을 제곱 하며 각 단계에서 지수를 절반으로 줄여서 곱셈의 횟수를 줄이는 것 입니다.
- 제일 먼저 result를 1로 초기화 합니다. 이후 지수(pow)가 0보다 클 동안 계속해서 반복문을 수행 합니다.
- 지수(pow)가 홀수인 경우에는 기본값(base)을 곱합니다. (추가로 모듈러 연산을 합니다)
- 기본값을 제곱 합니다. (추가로 모듈러 연산을 합니다)
- 지수(pow)는 2로 나눕니다.
base값을 제곱 했기 때문
위의 A¹³ 의 예시와 연관지어서 코드를 풀이해보겠습니다.
첫번째 반복문에서 pow의 값은 13 입니다. 홀수 값이죠. if(pow%2==1) 조건에 들어갑니다.
13 = (이진수) 1101에서 맨 마지막 1에 해당
그렇기 때문에 result(1)에 현재 base 값(A) 를 곱해줍니다. 반복을 마치며 base는 제곱이 됩니다. (A²)
두번째 반복에서는 pow의 값이 6이 되었습니다. 이진수 1101 에서 뒤에서 두번째 자리에 해당하는 것(0) 처럼 짝수 값입니다.
이때는, result(A) 값에는 변화가 없고 base만 제곱시키고 다음 반복으로 넘어갑니다 (A⁴)
A¹³ = A⁸ * A⁴ * A¹를 확인 해 보면 A² 은 없는게 확인 됨.
세번째 반복 에서 pow 값은 3입니다. A⁴를 곱해주겠죠. result는 A * A⁴ 이 됩니다. base는 제곱이 되며 A⁸ 이 됩니다.
네번째에서는 pow가 1이라서 result(A * A⁴) 에는 base (A⁸) 을 곱해주겠죠. result는 ``A¹ * A⁴ * A⁸가 되고 base는A¹⁶` 이 됩니다.
그러고나서 이제 pow는 0이 되며 본인의 생명 주기의 끝을 맞이합니다.
최종 결과값 result는 곱셈의 순서는 바뀌었지만 위에서 알아본 것 처럼 A¹ * A⁴ * A⁸ 가 되었네요.
A¹³ 의 예시를 들으며 모듈러 연산은 따로 언급하지 않았지만, 오버플로를 피하기 위해 매 계산마다 꾸준히 모듈러를 진행 합니다. result 뿐만 아니라 base도 계속해서 제곱되는 값이다보니 값이 엄청나게 커지거든요.
최종적으로 성능 테스트를 진행 해 보았습니다.
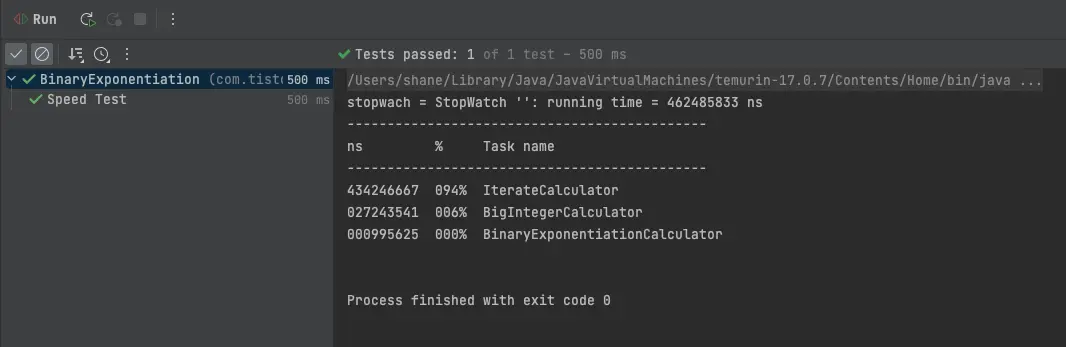
InterateCalculator가 가장 느렸고, 그 다음으로 BigIntegerCalculator는 처음꺼보다야 훨씬 빨랐지만, 가장 나중에 진행한 이진 거듭제곱 방법이 압도적인 성능을 자랑합니다.
BinaryExponentiationCalculator 가 100점의 퍼포먼스 점수를 받았다 치면, BigIntegerCalculator 는 약 3.65점이고, IterateCalculator는 0.23 점이니 비교가 불가능 할 정도입니다.
사실 쉬운 개념이 아니고 수학적인 개념이었습니만 프로그래밍에서도 RSA 암호화나 그래프 이론 혹은 그래픽 분야 등 행렬 거듭제곱이 필요한 필드에서 활용한다면 엄청난 성능상 이점을 거둘 수 있겠습니다.
감사합니다.
본문에 작성한 코드 전문은 https://github.com/ShanePark/markdownBlog/commit/aede226d6e01c2f105ec9bdc4d464d022ace4d29 에서 확인하실 수 있습니다.
References
'Development > Fundamentals' 카테고리의 다른 글
| java로 작성해보는 정렬 알고리즘과 성능 비교 (0) | 2021.08.03 |
|---|---|
| 네트워크 표준 모델 OSI 7 계층 ( OSI 7 Layer) (0) | 2021.07.22 |
| 객체지향설계 5대원칙 SOLID (4) | 2021.04.11 |
| 이진 탐색 알고리즘 (Binary search) (0) | 2021.01.17 |