Intro

재미삼아 취미로 시간 날때마다 한 두 문제씩 풀었던 programmers의 코딩 테스트 연습이 어느덧 100문제를 넘어갔습니다.
for문과 배열만 있다면 어떤 문제든 해결 할 수 있다고 말씀해주신 학원 초급 자바선생님의 말씀대로, 왠만한 문제는 머리속으로 떠올린 아이디어를 간단하게 노트에 적어 구체화 시킨 후에 그것을 IDE 상에 코드로 구현을 하면 해결되지 않는 문제가 없었습니다.
하지만 어느순간부터는 빈번히 막히는 일이 발생했고, 이제는 문제를 만났을때 "n중 for문 으로 풀어야지!" 라는 말도 안되는 해결 방안이 제시되기 시작했습니다. 그간 외면했던 DFS/ BFS를 정면으로 마주해야 하는 순간입니다. (물론 탐색하는 과정은 결국 동일합니다)
DFS
DFS는 깊이우선 탐색 Depth First Search 의 약자입니다.
트리나 그래프에서 한 루트로 검색하다가 특정 상황에서 최대한 깊숙히 들어가서 확인 한 뒤, 다시 돌아가 다른 루트를 탐색하는 방식입니다. 미로찾기를 생각하면 쉬운데요, 한 방향으로 끝까지 들어갔다가 막다른 길에 다다르면 (트리의 바닥에 도착) 왔던 길을 돌아가서 다른 방향으로 갑니다. 이 일을 찾는 값이 나올 때까지 혹은 모든 트리를 순회 할 때 까지 반복합니다. Stack이나 재귀함수를 이용해 구현합니다.
미로찾기를 하는데 루프(길이 막히지 않고 왔던길을 또 오는 경우)가 발생한다면 DFS는 해당 가지를 탈출 할 수 없습니다. 이럴때는 중복검사를 하거나 BFS를 고려해야 하는데요, 이런 DFS의 특징을 잘 기억하고 몇 가지 코드를 예로 실습해보겠습니다.
주사위굴리기
간단한 주사위 굴리기로 시작하겠습니다.
프로그래밍에 처음 입문할 때 한번씩 짜보게 되는 코드입니다.
1. 주사위 굴리기 구현
Math.random() 함수를 이용하겠습니다. Math.random() 함수는 Math 클래스에 static 메서드로 아래와 같이 구현 되어 있습니다.
java /** * Returns a {@code double} value with a positive sign, greater * than or equal to {@code 0.0} and less than {@code 1.0}. * Returned values are chosen pseudorandomly with (approximately) * uniform distribution from that range. * * <p>When this method is first called, it creates a single new * pseudorandom-number generator, exactly as if by the expression * * <blockquote>{@code new java.util.Random()}</blockquote> * * This new pseudorandom-number generator is used thereafter for * all calls to this method and is used nowhere else. * * <p>This method is properly synchronized to allow correct use by * more than one thread. However, if many threads need to generate * pseudorandom numbers at a great rate, it may reduce contention * for each thread to have its own pseudorandom-number generator. * * @apiNote * As the largest {@code double} value less than {@code 1.0} * is {@code Math.nextDown(1.0)}, a value {@code x} in the closed range * {@code [x1,x2]} where {@code x1<=x2} may be defined by the statements * * <blockquote><pre>{@code * double f = Math.random()/Math.nextDown(1.0); * double x = x1*(1.0 - f) + x2*f; * }</pre></blockquote> * * @return a pseudorandom {@code double} greater than or equal * to {@code 0.0} and less than {@code 1.0}. * @see #nextDown(double) * @see Random#nextDouble() */ public static double random() { return RandomNumberGeneratorHolder.randomNumberGenerator.nextDouble(); }
계속 코드를 파고 들면 Random 이라는 클래스도 나오고, seedUniquifier와 System.nanoTime() 을 비트연산 해서 랜덤값을 생성하는 것을 확인 할 수 있는데, 지금의 코드작성에는 0 <= Math.random() < 1 의 double 타입 값을 반환한다는 것만 알면 충분합니다.
javapublic class Dice { public static void main(String[] args) { Dice dice = new Dice(); System.out.println(dice.play()); } public int play(){ return (int) ((Math.random() * 6) + 1); } }
간단한 주사위 게임 코드 입니다. 코드를 실행하면 1~6 중 하나의 값을 출력 해 주도록 했습니다.
주사위를 한번 굴렸을때의 모든 경우의 수는 {1,2,3,4,5,6} 총 6개 입니다.
2. 주사위 두번 굴리기
그러면 이번엔 주사위를 두번 돌려보겠습니다.
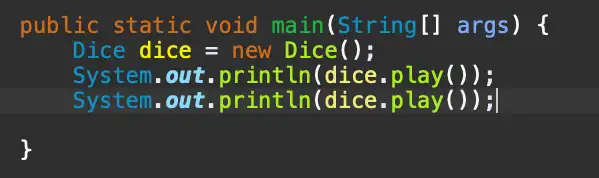
dice.play() 를 한번만 더 호출 했습니다. 결과는 4와 3이 나왔네요.
3. 경우의 수
이번에는 주사위를 두 번 굴렸을 경우의 경우의 수를 모두 구해보겠습니다.
여러가지 구현 방법이 있겠지만 이중 for문을 이용해보도록 하겠습니다.
주사위를 1개 굴렸을 때의 경우의수가 {1,2,3,4,5,6} 이었는데요, 이를 배열로 만들어두고, 이중 for문으로 경우의 수 만큼 반복하며 모든 경우의 수를 구해 보도록 하겠습니다.
javapublic class Dice2Possibility { public static void main(String[] args) { int[] dice = {1,2,3,4,5,6}; final int length = dice.length; for(int i=0; i<length; i++) { for(int j=0; j<length; j++) { System.out.printf("{%d,%d}",dice[i],dice[j]); } } } }
코드는 이렇게 작성 했습니다, 결과를 확인하면
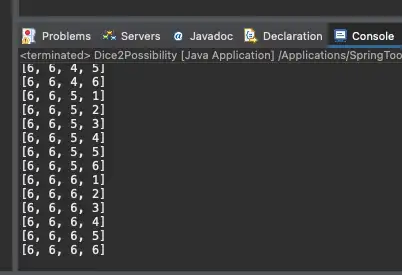
이렇게 나왔습니다. {1,1} 부터 {6,6} 까지 총 36가지의 경우의 수가 있습니다.
4. 3번 굴리기
이번에는 주사위를 3번 굴려보겠습니다.
javapublic class Dice2Possibility { public static void main(String[] args) { int[] dice = {1,2,3,4,5,6}; final int length = dice.length; int count = 0; for(int i=0; i<length; i++) { for(int j=0; j<length; j++) { for(int k=0; k<length; k++){ System.out.printf("{%d,%d,%d}\n",dice[i],dice[j],dice[k]); count++; } } } System.out.println(count); } }
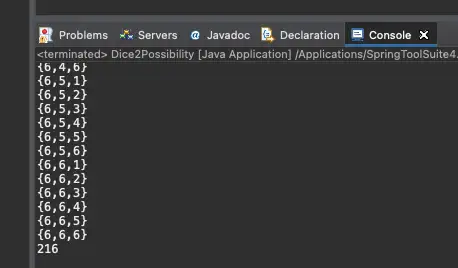
위와 같이 총 216 가지의 경우의 수가 존재합니다.
5. n 번 굴리기
이번에는 주사위를 총 n 번 던졌을 때의 모든 경우의 수를 확인하는 프로그램을 만들어 보겠습니다.**
위에서 여태 작성한 코드들이 의미가 없어집니다. 일단 정확히 몇번의 주사위를 던진다는 것을 알았을때는 코드의 완성도를 떠나 어쨌든 반복문을 n번 겹친다면 구현은 할 수 있었지만 n번에 대한 정보를 동적으로 받아온다면 코드에 n번의 반복문을 작성할 수 없습니다.
이제 DFS의 풀이가 필요합니다.
일단 제가 작성한 전체 코드를 먼저 보고, 어떤식으로 구현했는지 설명 해 드리겠습니다.
javaimport java.util.Arrays; public class Dice2Possibility { public static void main(String[] args) { play(4); } public static void dfs(int[] output,int depth, int n) { if(depth == n) { System.out.println(Arrays.toString(output)); return; } for(int i=1; i<=6; i++) { output[depth] = i; dfs(output, depth+1, n); } } public static void play(int n) { int[] output = new int[n]; dfs(output, 0, n); } }
실행 결과는 아래와 같습니다. 총 4번 주사위를 굴렸으니 6^4 으로 1296 가지의 경우의 수가 존재합니다.

main 메서드
java public static void main(String[] args) { play(4); }
일단 메인 메서드에서는 play 메서드를 호출 했습니다. 몇번 주사위를 돌릴건지를 인자로 받습니다. 그래서 주사위를 4번 돌리기 위해 play(4)를 호출 해 보았습니다.
play 메서드
java public static void play(int n) { int[] output = new int[n]; dfs(output, 0, n); }
특별한건 없고, 입력받은 n 사이즈의 output int 배열만을 만들어서,
dfs 메서드를 호출 했습니다. 입력값으로 output, 0(기본depth), n(주사위 굴릴 횟수) 만을 받습니다.
dfs 메서드
java public static void dfs(int[] output,int depth, int n) { if(depth == n) { System.out.println(Arrays.toString(output)); return; } for(int i=1; i<=6; i++) { output[depth] = i; dfs(output, depth+1, n); } }
dfs 메서드 입니다. 사실 조건이 워낙에 간단하다보니 메서드가 간단하게 구현 되었는데요, 중복이나 순서 등 조건이 추가되면 방문했는지 여부를 확인하면서 해야 해서 코드가 조금은 더 복잡해 집니다.
1) 첫 if 문에서는 지금까지 파고 들어온 depth가 주사위를 굴릴 횟수와 같은지 확인합니다. 필요한 만큼 주사위를 굴렸다면, output 배열에는 필요한 데이터가 모두 쌓였기 때문에 그대로 출력 해 주고 return으로 메서드를 종료시킵니다.
2) if문에 걸리지 않았다면, 주사위를 굴렸을때 나오는 값인 1~6까지 반복하며 이번 depth의 자리에 해당 값을 넣어 줍니다. 그러고나서 만든 output 배열과, 다음 depth, 그리고 주사위를 굴릴 총 횟수인 n을 인자로 하여 다시 한번 dfs 함수를 호출 해 줍니다.
이렇게 하면 depth를 한번 거칠 때 마다 총 6번의 dfs 메서드를 호출 하게 됩니다.
소수찾기
이번엔 주사위 굴리기를 했으니 조금 더 어려운 dfs를 구현 해 보도록 하겠습니다.
프로그래머스의 2단계 문제인 "소수찾기" 에 필요한 순열 문제를 해결 해 보도록 하겠습니다.
문제
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.
각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이 조각으로 만들 수 있는 소수가 몇 개인지 return 하도록 solution 함수를 완성해주세요.
*제한사항
numbers는 길이 1 이상 7 이하인 문자열입니다.numbers는 0~9까지 숫자만으로 이루어져 있습니다."013"은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미입니다.
접근
해당 문제를 해결하기 위해서는 일단 해당 종이 조각들을 어떤 순서로 나열 할 건지에 대한 모든 경우의 수를 체크 해야 한다고 생각했습니다. 총 3개의 종이조각이 있다면 해당 종이 조각들을 3의 크기로 나열하는데는 123, 132, 213, 231, 312, 321 이렇게 총 6가지의 경우의 수가 발생합니다. 하지만 여기에서 끝나지 않고 2의 크기 나열인 [1,2], [1,3], [2,1], [2,3], [3,1], [3,2] 도 고려해야 하며 1의 크기 나열인 1, 2, 3도 모두 고려해야 합니다.
종이 조각들의 순서에 따른 모든 경우의 순열을 DFS를 활용해 만들어 보도록 하겠습니다.
이 경우는 위의 주사위때와는 상황이 많이 다릅니다. 주사위 에서의 방식으로 123을 3개로 나열하면 3의 3제곱, 총 27가지의 경우의 수가 발생합니다. 이번에는 그때와는 다르게 한번 사용된 숫자는 다시 사용되지 않습니다. 해당 상황을 해결하기 위해 visited 배열을 만들어서 사용합니다. 그리고 또한 n의 크기로만 나열하지 않고 1~n의 크기 나열을 모두 고려해야 합니다.
dfs로 모든 순열을 확인 하고, 해당 순열의 순서로 글자를 나열 한 뒤 그 숫자를 Set에 저장하도록 코드를 작성하겠습니다.
numbers에는 다른 자리에 같은 숫자가 들어갈 수 있기 때문에 중복된 숫자를 만들었을 경우를 대비해서 Set으로 만듭니다.
코드
solution 메서드
java public static void solution(String numbers) { // 만들 수 있는 모든 경우의 Integer들을 모을 Set Set<Integer> set = new HashSet<>(); // 0부터 length-1 까지의 숫자 배열을 만든다. final int length = numbers.length(); int[] arr = new int[length]; for(int i=0; i<length; i++) { arr[i] = i; } // 만들 수 있는 모든 길이의 순열을 만든다. boolean[] visited = new boolean[length]; for(int i=1; i<=length; i++) { int[] output = new int[i]; dfs(arr, output, visited, 0, i, numbers, set); } System.out.println(set); }
일단 필요한 set과 숫자 배열을 생성 합니다. 배열의 길이에 해당하는 visited boolean 배열도 만들어줍니다.
그러고는 반복문을 통해 크기가 1개짜리 순열부터 numbers의 길이와 동일한 크기의 순열까지 모두 만들어줍니다.
마지막에는 그렇게 모은 set을 출력해주며 함수가 종료됩니다.
dfs 메서드
java static void dfs(int[] arr, int[] output, boolean[] visited, int depth, int length, String numbers, Set<Integer> set) { if(depth == length) { StringBuffer sb = new StringBuffer(); for(int i : output) { sb.append(numbers.charAt(i)); } set.add(Integer.parseInt(sb.toString())); }else { for(int i=0; i<numbers.length(); i++) { if(visited[i] != true) { visited[i] = true; output[depth] = arr[i]; dfs(arr, output, visited, depth+1, length, numbers, set); visited[i] = false; } } } }
찾고자 하는 순열의 크기와 depth가 일치 할 경우에는, numbers 스트링을 해당 순열에 맞춰 배열 한 뒤에 Integer로 parsing 해서 set에 추가 합니다.
if문에 들어가지 않을 경우에는 else 문에서, dfs 방식으로 방문하지 않은 순번을 방문하고 또 다시 dfs를 호출하도록 했습니다.
전체 코드
javaimport java.util.HashSet; import java.util.Set; public class Permutation { public static void main(String[] args) { solution("011"); } public static void solution(String numbers) { // 만들 수 있는 모든 경우의 Integer들을 모을 Set Set<Integer> set = new HashSet<>(); // 0부터 length-1 까지의 숫자 배열을 만든다. final int length = numbers.length(); int[] arr = new int[length]; for(int i=0; i<length; i++) { arr[i] = i; } // 만들 수 있는 모든 길이의 순열을 만든다. boolean[] visited = new boolean[length]; for(int i=1; i<=length; i++) { int[] output = new int[i]; dfs(arr, output, visited, 0, i, numbers, set); } System.out.println(set); } static void dfs(int[] arr, int[] output, boolean[] visited, int depth, int length, String numbers, Set<Integer> set) { if(depth == length) { StringBuffer sb = new StringBuffer(); for(int i : output) { sb.append(numbers.charAt(i)); } set.add(Integer.parseInt(sb.toString())); }else { for(int i=0; i<numbers.length(); i++) { if(visited[i] != true) { visited[i] = true; output[depth] = arr[i]; dfs(arr, output, visited, depth+1, length, numbers, set); visited[i] = false; } } } } }
그렇게 짠 전체 코드입니다. 실행했을때의 결과는 아래와 같습니다.
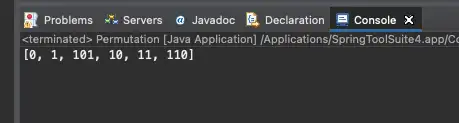
이제 이 중에 소수인 숫자는 101, 11 이렇게 두개입니다.
혹시 프로그래머스의 문제를 풀고자 하는 분은 여기에서 해당 set을 순회 하며
java static public boolean isPrime(int number) { if(number == 2) return true; if(number<2 || number%2==0) return false; for(int i=3; i<=Math.sqrt(number); i+=2) { if(number % i == 0) { return false; } } return true; }
위와 같은 코드로 소수인지를 체크 한 뒤에, true가 되는 모든 set의 원소의 갯수를 구하면 됩니다.
마치며
최대한 간단히 정리한다고 해 보았지만, 실제로 DFS가 응용되면 더 복잡한 코드가 될 수도 있으며 많은 상당히 많은 문제를 해결하는데 사용 될 수 있는 코드 입니다.
추가로 공부한 DFS 연습을 한번 해 보고 싶다면
https://programmers.co.kr/learn/courses/30/lessons/1835
해당 문제를 추천드립니다. 풀이한 분이 그렇게 많지는 않은데 문제가 제법 재밌더라고요.
더 재밌는건, 이 문제는 n이 정해진 문제다 보니 n중 for문으로 진짜 푼 분들이 계신다는 겁니다.
하지만 DFS로 접근해보세요! 이상입니다.
'Development > Problem Solving' 카테고리의 다른 글
| Leetcode) 소개 및 풀이 코드 Github에 자동 커밋방법 (0) | 2022.01.16 |
|---|---|
| 문제풀이: 가장 긴 팬린드롬(palindrome) (0) | 2021.12.18 |
| JAVA로 알아보는 힙 (Heap) 자료구조 (0) | 2021.10.16 |
| 피보나치 수열과 프로그래머스 땅따먹기 문제로 알아보는 Dynamic Programming (동적 프로그래밍) (0) | 2021.07.31 |
| 무한깊이 그리고 너비우선탐색 BFS (0) | 2021.07.28 |