JAVA로 알아보는 힙 (Heap) 자료구조

작성: 2021.10.16

수정: 2021.10.16

읽는시간: 00 분

Development/Problem Solving

반응형

Heap

Heap은 최소값 및 최대값을 최대한 빠르게 찾아내기 위해 특별히 고안된 자료 구조 입니다. 완전 이진트리(마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리의 형태)를 기본으로 하고 있으며, 그 목적에 걸맞게 두개의 타입으로 나뉩니다.

  1. Max-Heap

Max-Heap 에서 root 노드의 key는 무조건 해당 노드의 자식 노드들의 key보다 크거나 같습니다. 또한 같은 속성이 모든 sub-tree 들에게도 재귀적으로 적용됩니다.

간단히 말해 Max-Heap 트리에서 자식 노드에 딸린 트리 하나 하나가 모두 Max-Heap의 조건을 만족합니다.

  1. Min-heap

Min-Heap 에서는 반대로 root 노드의 키값이 모든 자식들의 키 보다 작거나 같습니다.

또한 재귀적으로 자식 트리들 하나하나 모두 해당 조건을 만족합니다.

​

그림으로 예를 들어보겠습니다.

1

https://en.wikipedia.org/wiki/Heap_(data_structure)

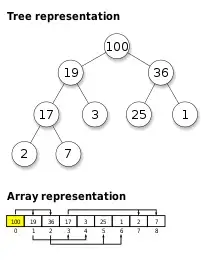
가장 큰 값이 root로 가는 Max-Heap 입니다. 그림을 보며 쉽게 헷갈릴 수 있는데, 키값의 대소 관계는 부모노드와 자식 노드 사이에만 성립합니다. 형제 노드 간의 위치는 크기와 전혀 관계가 없습니다. 오로지 "최대값" 혹은 "최소값"을 찾기 위한 그 목적에 충실한 자료구조입니다. 자식 노드가 여러개인 형태의 힙을 사용 할 수도 있겠지만 보통은 자식 노드의 갯수가 최대 2개인 binary heap을 사용합니다.

위에서 볼 수 있는 것 처럼 root 에 있는 100 은 그 어느 자손 node 보다도 큰 값을 가지고 있습니다. 또한 그 아래에 있는 19 값을 가진 노드도 그 자식들 보다 값이 크며 그 자식 노드로 있는 17 또한 같은 조건을 만족 합니다.

19(좌)<36(우) 의 경우와 17(좌)>3(우) 의 경우에서 확인 할 수 있는 것 처럼 형제 노드들 간의 값 비교는 의미가 없습니다.

가장 아래의 Array representation은 노드를 배열 형태로 표현 한 것인데요, 빈 공간이 없는 완전 이진트리기 때문에 굳이 트리 형태가 아닌 배열로 표현하는 것이 가능합니다.

​

JAVA로 Min-Heap 직접 구현

배열로 구현 해 보겠습니다. 일단 간단한 메서드들을 먼저 만듭니다.

package com.tistory.shanepark;

public class Heap {
    private int capacity = 10;
    private int size = 0;

    int[] items = new int[capacity];

    private int getLeftChildIndex(int parentIndex) {
        return 2 * parentIndex + 1;
    }

    private int getRightChildIndex(int parentIndex) {
        return 2 * parentIndex + 2;
    }

    private int getParentIndex(int childIndex) {
        return (childIndex - 1) / 2;
    }

    private boolean hasLeftChild(int index) {
        return getLeftChildIndex(index) < size;
    }

    private boolean hasRightChild(int index) {
        return getRightChildIndex(index) < size;
    }

    private boolean hasParent(int index) {
        return getParentIndex(index) >= 0;
    }

    private int leftChild(int index) {
        return items[getLeftChildIndex(index)];
    }

    private int rightChild(int index) {
        return items[getRightChildIndex(index)];
    }

    private int parent(int index) {
        return items[getParentIndex(index)];
    }

}

​

index에 대한 이해를 돕기 위해 아래의 그림을 준비 했습니다. 제가 보라색으로 써 넣은 숫자가 배열에서의 각각의 인덱스 입니다. 부모노드의 index에 2를 곱하고, 거기에 1을 더한게 leftChild의 index, 2를 더한게 rightChild의 인덱스 입니다. 인덱스 번호에서 1을 뺀 뒤에 2로 나누면 부모의 index를 찾을 수도 있습니다.

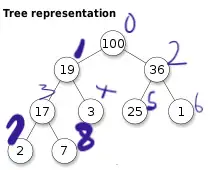
image-20211016172947891

​

​

배열의 크기가 꽉 찼을때에는 배열의 크기를 2배로 늘리는 메서드도 추가해 줍니다.

private void ensureExtraCapacity() {
  if (size == capacity) {
    items = Arrays.copyOf(items, capacity * 2);
    capacity *= 2;
  }
}

​

이번엔 peek 메서드 입니다. root 의 값을 얻어오며, 힙 트리의 크리가 0 이라면 예외를 호출합니다.

public int peek() {
  if (size == 0) throw new IllegalStateException();
  return items[0];
}

​

이번에는 poll 메서드입니다. 지금부터 다소 복잡해집니다.

public int poll() {
  if (size == 0) throw new IllegalStateException();

  // 1
  int item = items[0];

  // 2
  items[0] = items[size - 1];

  // 3
  size--;

  // 4
  heapifyDown();

  // 5
  return item;
}

조금 복잡하니 순서대로 설명하겠습니다.

  1. 일단 반환할 값을 item 이라는 변수에 담아 줍니다.
  2. root의 값을 내보내면 그 칸이 비어버립니다. 그러니 일단 가장 마지막에 있는 노드를 가져와 root에 담습니다.
  3. 하나의 값이 빠져나갔으니 사이즈를 한개 줄입니다.
  4. root 에 올라간 값이 최소값이라는 규칙이 깨졌으니 아래로 내려오며(heapifyDown) 재정렬 합니다.
  5. 마지막으로 아까 저장해둔 item 을 반환합니다.

아직 heapifyDown 메서드는 만들지 않았습니다.

​

이번에는 add 메서드 입니다.

public void add(int item) {
  ensureExtraCapacity();
  items[size] = item;
  size++;
  heapifyUp();
}

새로운 노드를 추가 할 때는 일단 아까 추가한 ensureExtraCapacity 메서드를 호출 해서 배열이 충분한 크기임을 확실하게 합니다. 이후 마지막 자리인 items[size] 에 item을 넣어 주고, 총 size를 한개 늘려 줍니다. items[size++] = item 라고 써도 되겠네요.

다 끝났으면 이제 최종적으로 가장 마지막에 추가 한 노드를 위로 올리며 정렬이 필요하면 다시 정렬 시킵니다.

​

이번에는 아까 만들지 않고 넘어갔던 던 heapifyUp 메서드를 구현합니다.

private void heapifyUp() {
  int index = size - 1;
  while (hasParent(index) && parent(index) > items[index]) {
    swap(getParentIndex(index), index);
    index = getParentIndex(index);
  }
}

index 를 가장 마지막 노드로 잡고 시작합니다. 마지막에 추가한 노드를 위로 올리는 과정이기 때문입니다.

그 인덱스부터 parent가 있고 또한 그 parent의 키 값이 지금 확인중인 노드의 키 값보다 큰 경우에는 서로 스왑 해 줍니다. 그러고 인덱스를 새로 스왑한 자리로 바꿔 더이상 스왑이 없을 때까지 계속 반복문을 태웁니다.

​

이번엔 반대인 heapifyDown 메서드 입니다. 

private void heapifyDown() {
  int index = 0;
  while (hasLeftChild(index)) {
    int smallerChildIndex = getLeftChildIndex(index);
    if(hasRightChild(index) && rightChild(index) < leftChild(index)) {
      smallerChildIndex = getRightChildIndex(index);
    }

    if(items[index] < items[smallerChildIndex]){
      break;
    } else {
      swap(smallerChildIndex, index);
      index = smallerChildIndex;
    }
  }
}

위에서 부터 아래로 내려가며 검증 하는데요. root 에서 시작하기 때문에 index는 0 에서 시작합니다.

hasLeftChild를 검사 하는 이유는, rightChild가 있으면 무조건 leftChild가 있지만, rightChild가 없으면서 leftChild는 있는 경우가 있기 때문입니다.

한개씩 트리 depth를 내려 가면서 smallerChild와 비교 하는데요, smallChild의 경우에는 leftChild와 rightChild를 비교해 더 작은 child의 index를 미리 기록 해 둡니다.

그러고 index의 키값과 smallerChild의 키값을 비교해서, smallerChild의 키값이 더 크다면 더이상 내려갈 필요가 없기 때문에 break를 하고요, 그렇지 않은 경우에는 smallerChild와 swap을 시켜 주고, 인덱스를 새로운 자리로 옮겨 준 뒤에 계속해서 heapifyDown 로직을 이어갑니다.

​

사실 그림으로 이해하는게 가장 쉬우니 종이에 새로운 Node를 추가하거나, root의 노드를 빼는 과정을 직접 그려보는게 가장 도움이 됩니다.

​

마지막으로 swap 메서드를 구현 합니다. 크게 어렵지 않으니 따로 설명은 하지 않겠습니다.

private void swap(int smallerChildIndex, int index) {
  int temp = items[smallerChildIndex];
  items[smallerChildIndex] = items[index];
  items[index] = temp;
}

​

테스트

열심히 함께 직접 구현해 본 Heap 을 테스트 해볼 시간입니다. 기대됩니다.

​

일단 힙 테스트를 하며 중간중간 확인을 위해 printHeap 메서드를 만들어 주었습니다. 

public void printHeap() {
  System.out.println(Arrays.toString(items));
}

​

메인메서드를 테스트를 위해 대강 만들어 보았습니다. 

public static void main(String[] args) {
  Heap heap = new Heap();
  heap.add(2);
  heap.printHeap();
  heap.add(4);
  heap.printHeap();
  heap.add(1);
  heap.printHeap();
  heap.add(5);
  heap.printHeap();
  heap.add(0);
  heap.printHeap();
  System.out.println(heap.poll());
  heap.printHeap();
  System.out.println(heap.peek());
}

​

작동 결과

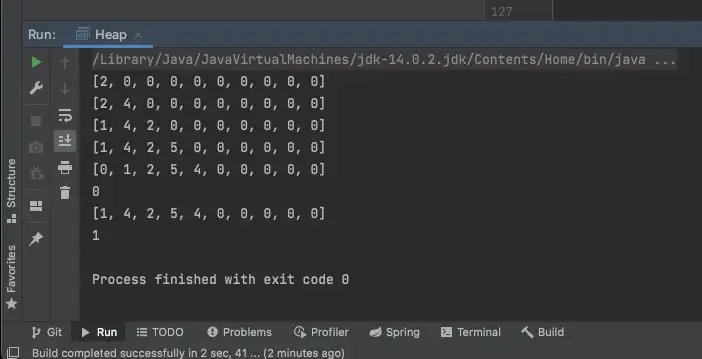
image-20211016185716389

​

잘 작동되었는지 눈으로 보기엔 확인이 쉽지 않죠? 그림으로 직접 그려 보았습니다.

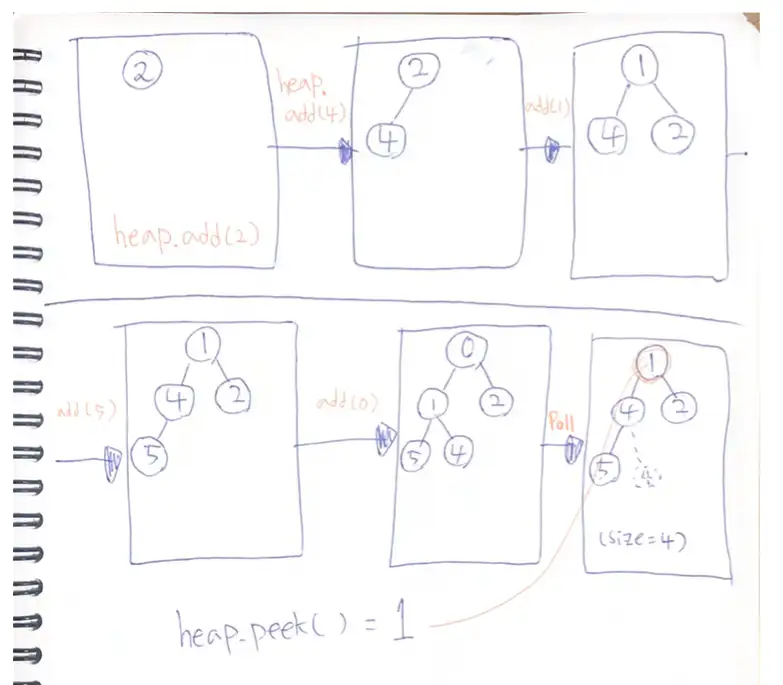
image-20211016190630060

6번째 네모 박스에서 poll 이후에 4가 두개 있는 것 처럼 보이는데, size 가 줄었기 때문에 그 자리는 사실 없는 숫자 입니다.

그래도 눈에 보이면 헷갈릴 수 있으니 size만 줄이지 않고 실제 값도 제거한다면,

public int poll() {
  if (size == 0) throw new IllegalStateException();
  int item = items[0];
  items[0] = items[size - 1];
  items[size-1] = 0;
  size--;
  heapifyDown();
  return item;
    }

poll 메서드에 위와 같이 items[size-1] 을 추가해줄 수 있습니다.

​

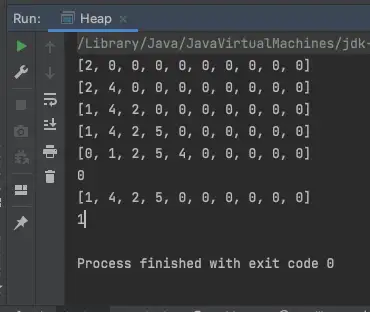
image-20211016190921296

이제 poll 이후에 4가 말끔하게 제거 됩니다.

​

의도 한 대로 함께 만들어 본 Heap이 잘 작동 합니다. 위의 코드 전문을 올려드리겠습니다.

Heap.java

package com.tistory.shanepark;

import java.util.Arrays;

public class Heap {
    private int capacity = 10;
    private int size = 0;

    int[] items = new int[capacity];

    private int getLeftChildIndex(int parentIndex) {
        return 2 * parentIndex + 1;
    }

    private int getRightChildIndex(int parentIndex) {
        return 2 * parentIndex + 2;
    }

    private int getParentIndex(int childIndex) {
        return (childIndex - 1) / 2;
    }

    private boolean hasLeftChild(int index) {
        return getLeftChildIndex(index) < size;
    }

    private boolean hasRightChild(int index) {
        return getRightChildIndex(index) < size;
    }

    private boolean hasParent(int index) {
        return getParentIndex(index) >= 0;
    }

    private int leftChild(int index) {
        return items[getLeftChildIndex(index)];
    }

    private int rightChild(int index) {
        return items[getRightChildIndex(index)];
    }

    private int parent(int index) {
        return items[getParentIndex(index)];
    }

    private void ensureExtraCapacity() {
        if (size == capacity) {
            items = Arrays.copyOf(items, capacity * 2);
            capacity *= 2;
        }
    }

    public int peek() {
        if (size == 0) throw new IllegalStateException();
        return items[0];
    }

    public int poll() {
        if (size == 0) throw new IllegalStateException();
        int item = items[0];
        items[0] = items[size - 1];
        items[size - 1] = 0;
        size--;
        heapifyDown();
        return item;
    }

    public void add(int item) {
        ensureExtraCapacity();
        items[size] = item;
        size++;
        heapifyUp();
    }

    private void heapifyUp() {
        int index = size - 1;
        while (hasParent(index) && parent(index) > items[index]) {
            swap(getParentIndex(index), index);
            index = getParentIndex(index);
        }
    }

    private void heapifyDown() {
        int index = 0;
        while (hasLeftChild(index)) {
            int smallerChildIndex = getLeftChildIndex(index);
            if (hasRightChild(index) && rightChild(index) < leftChild(index)) {
                smallerChildIndex = getRightChildIndex(index);
            }

            if (items[index] < items[smallerChildIndex]) {
                break;
            } else {
                swap(smallerChildIndex, index);
                index = smallerChildIndex;
            }
        }
    }

    private void swap(int smallerChildIndex, int index) {
        int temp = items[smallerChildIndex];
        items[smallerChildIndex] = items[index];
        items[index] = temp;
    }

    public void printHeap() {
        System.out.println(Arrays.toString(items));
    }

    public static void main(String[] args) {
        Heap heap = new Heap();
        heap.add(2);
        heap.printHeap();
        heap.add(4);
        heap.printHeap();
        heap.add(1);
        heap.printHeap();
        heap.add(5);
        heap.printHeap();
        heap.add(0);
        heap.printHeap();
        System.out.println(heap.poll());
        heap.printHeap();
        System.out.println(heap.peek());
    }

}

​

저도 힙을 직접 작성해보는건 처음인데 의도대로 작동 하는 걸 보니 재밌습니다.

​

PriorityQueue

그렇다면 Java 에서 Heap 자료구조를 사용하려면 어떻게 해야 할까요? java에서 구현되어 있는 라이브러리가 있을까요?

그 정답은 위에 써있는 것 처럼 java에서는 Java1.5 부터 PriorityQueue로 Heap을 구현 해 두었습니다.

자바 공식 문서 https://docs.oracle.com/javase/7/docs/api/java/util/PriorityQueue.html

​

한번 바로 사용 해 보겠습니다.

package com.tistory.shanepark.heap;

public class PriorityQueue {
    public static void main(String[] args) {

        java.util.PriorityQueue<Integer> minHeap = new java.util.PriorityQueue<>();
        minHeap.add(2);
        minHeap.add(0);
        minHeap.add(4);
        System.out.println(minHeap.poll());
        System.out.println(minHeap.poll());
        System.out.println(minHeap.poll());

    }
}

이렇게 2, 0 , 4 를 PriorityQueue 에 add 한 뒤에, 한 개 씩 꺼내어 출력 해 보면.

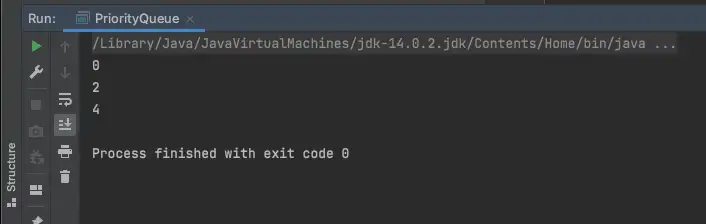
image-20211016201135309

가장 작은 값 부터 하나씩 출력 되는 것을 확인 하실 수 있습니다.

반대로 maxHeap을 만들려면 어떻게 해야 할까요?

기본적으로 PriorityQueue는 min-Heap 을 구현 해 두었는데요, 예전에 잘 몰랐을 때는 모든 수를 음수로 만들어서 max Heap 처럼 사용 했었는데 이번에 알고 보니 생성자에서 Comparator를 받더라고요.

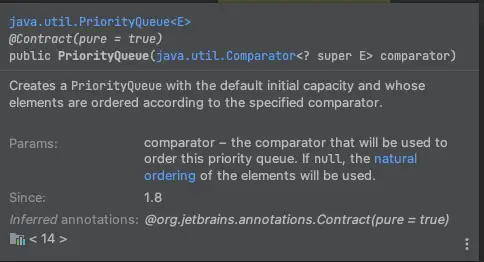
image-20211016201500145

이를 이용해서 Comparator를 반대로 구현 해 둔다면 max Heap도 문제 없이 만들 수 있습니다.

package com.tistory.shanepark.heap;

public class MaxHeap {
    public static void main(String[] args) {

        java.util.PriorityQueue<Integer> maxHeap = new java.util.PriorityQueue<>((o1, o2) -> Integer.compare(o2,o1));
        maxHeap.add(2);
        maxHeap.add(0);
        maxHeap.add(4);
        System.out.println(maxHeap.poll());
        System.out.println(maxHeap.poll());
        System.out.println(maxHeap.poll());

    }
}

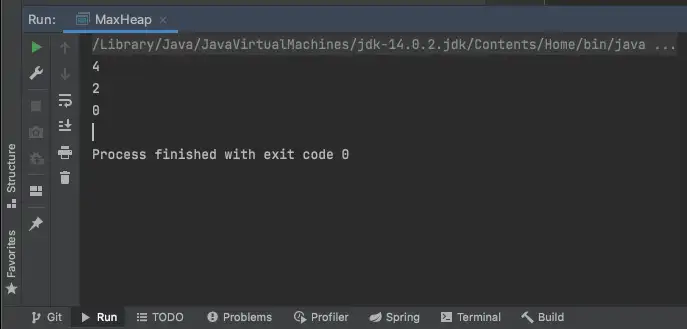
image-20211016201612911

​

Heap 자료구조를 사용하는 이유

처음에 말씀드렸던 것 처럼 Heap은 최소, 최대값을 구하는데 특화되어 있는 자료 구조 입니다. 루트의 값만 바로 가져오면 되기 때문에 O(1)의 시간 복잡도 만으로 바로 최대값이나 최소값을 찾을 수 있습니다.

​

새로운 값을 추가(add) 하거나 삭제(poll) 하는 경우에는 시간복잡도가 어떻게 될까요?

정답은 O(log n)인데요, 힙 트리의 높이가 h = log(2, n+1) 이며 연산을 최대 h-1 번 하게 되기 때문에 그렇습니다.

​

마무리

지금까지 Heap 자료구조에 대해 알아 보았습니다. 예전에 프로그래머스 Level 2 문제 더 맵게 를 풀 때, Heap을 사용하지 않고는 어떤 방법으로 풀어도 시간 초과가 뜨는 바람에 주말에 7시간 넘게 하루 종일 매달렸던 기억이 있습니다. 그때 이후로 Heap을 공부하고 정리 하겠다고 벼르고 벼르다가 드디어 한번 정리 해 보았습니다.

이번에 학습한 Heap을 사용하는 문제를 풀어 보고 싶다면 https://programmers.co.kr/learn/courses/30/parts/12117 에 방문해서 풀어 보시면 됩니다.

위에서 작성한 코드는 아래 링크에서 확인 하실 수 있습니다.

https://github.com/Shane-Park/markdownBlog/tree/master/projects/java/src/com/tistory/shanepark/heap

​

수고하셨습니다.

​

ref : HackerRank Youtube

https://www.youtube.com/watch?v=t0Cq6tVNRBA

반응형
저작자표시 비영리 변경금지

'Development > Problem Solving' 카테고리의 다른 글

Leetcode) 소개 및 풀이 코드 Github에 자동 커밋방법  (0) 2022.01.16
문제풀이: 가장 긴 팬린드롬(palindrome)  (0) 2021.12.18
피보나치 수열과 프로그래머스 땅따먹기 문제로 알아보는 Dynamic Programming (동적 프로그래밍)  (0) 2021.07.31
무한깊이 그리고 너비우선탐색 BFS  (0) 2021.07.28
n중 for문과 깊이우선탐색 DFS  (0) 2021.07.28

'Development/Problem Solving'의 다른글

티스토리툴바