Intro
알고리즘 문제를 풀 때 매우 많은 상황에서 주어진 데이터를 정렬해야 할 경우가 생깁니다. 기본적으로 길이 N의 배열에서 특정 수를 찾는다면, 일반적인 탐색으로는 N번의 비교가 필요하지만, 정렬이 된 데이터라면 log(N) 번의 비교만에 찾아 낼 수 있는 강력한 binary Search를 사용 할 수 있습니다.
프로그래밍을 처음 공부하거나 자료구조를 공부 할 때 기본적인 정렬 알고리즘을 여러가지 배우게 되는데요.
흔히 기본적으로 접하게 되는 정렬 알고리즘을 살펴 보면..
O(n²)인 정렬 알고리즘
- 버블 정렬
- 선택 정렬
- 삽입 정렬
O(n log n)인 정렬 알고리즘
- 병합 정렬
- 힙 정렬
- 퀵 정렬
정도가 있습니다. 자바에서 정렬의 경우에는 기본적으로 DualPivotQuicksort로 구현이 되어 있는데요.
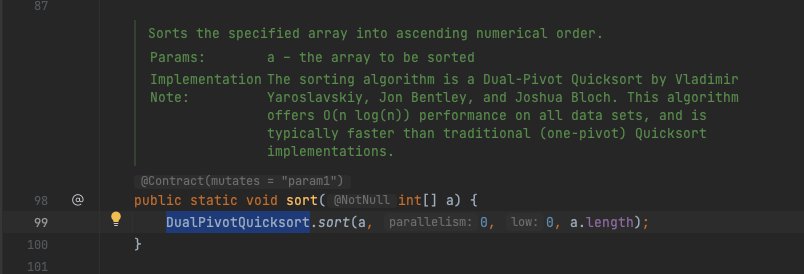
일반적인 Quick Sort의 경우에는 피벗이 최소값 혹은 최대값으로 계속 잡히는 최악의 경우 시간복잡도가 O(n²)이 되기 때문에, 그 단점을 보안하기 위해 언제나 O(n log n)을 보장해 줄 수 있도록 그런 선택을 한 것으로 보입니다. 주석에도 보통의 경우에 one-pivot Quicksort 보다 빠르다고 적혀 있습니다.
사실, 개발을 하다보면 직접 정렬 알고리즘을 구현해야 할 일은 흔하지 않고.. 극단적인 상황에서만 각 경우에 알맞은 정렬 알고리즘을 선택 할 수 있으면 충분할텐데요. 알고리즘 문제를 풀다 보면 그런 극단적인 상황이야말로 출제자들의 구미를 당기는 아주 좋은 먹잇감이기때문에 자주 접하게 됩니다.
그래서 이번에는 알고 있으면 종종 도움이 되는 카운팅 정렬Counting Sort)에 대해 이야기 해 보려고 합니다. 미리 말씀드리자면, 이 알고리즘은 정렬에 드는 시간이 겨우 O(N) 입니다.
문제
방금, 이 Counting Sort 알고리즘은 정렬에 O(N)의 뛰어난 시간복잡도를 자랑한다고 말씀 드렸는데요, 그런 좋은 성능의 정렬 알고리즘이 왜 대표적으로 쓰이지도 않고 흔히 알려지지도 않았을까 하는 궁금증이 생기는 분들이 계실거에요.
그 이유는, 카운팅정렬의 경우에는 활약할 수 있는 조건이 제법 까다롭기 때문입니다.
카운팅 정렬이 빛을 발할만한 정렬 문제를 내 보겠습니다.
대한민국에는 총 5천만명의 국민들이 살고 있습니다. 국민 전체의 형제자매 수 데이터가 int 배열로 주어집니다.
int[] siblings예 : [1, 2, 1, 0, 3, 1, ...]
티비에 나왔던 중랑구의 14남매가 가장 많은 형제자매라는 정보가 주어졌을 때, 형제자매 숫자로 오름차순 정렬된 길이 50,000,000의 int 배열을 반환하는
sortSiblings(int[] siblings)메서드를 구현 해 보세요.정렬 후 예: [0, 1, 1, 1, 2, 3]
사실 중국인구 14억으로 문제를 내서 O(n²)은 당연히 엄두도 못내고 O(n log n)도 통과가 힘들게 하고 싶었지만, 메모리 문제로 적당히 타협했습니다.
일단 간단하게 기본적인 배열 정렬 구현을 이용해서 문제를 해결해보겠습니다. 나중에 정렬 종류를 변경 할 수 있도록 정렬을 수행하는 Consumer 를 따로 받도록 메서드를 작성 했습니다.
package com.tistory.shanepark.sort;
import org.junit.jupiter.api.Test;
import java.util.Arrays;
import java.util.Random;
import java.util.function.Consumer;
import static org.assertj.core.api.Assertions.assertThat;
public class CountingSort {
final int POPULATION = 50_000_000;
final int MAX = 14;
@Test
public void compare() {
int[] siblings = randomArray();
long start1 = System.currentTimeMillis();
sortSiblings(siblings, (Consumer<int[]>) arr -> Arrays.sort(arr));
System.out.println("regular Sort" + ": " + (System.currentTimeMillis() - start1) + "ms");
}
private int[] randomArray() {
int[] arr = new int[POPULATION];
for (int i = 0; i < POPULATION; i++) {
arr[i] = new Random().nextInt(MAX);
}
return arr;
}
int[] sortSiblings(int[] siblings, Consumer sorter) {
sorter.accept(siblings);
return siblings;
}
}
실행 결과는 아래와 같습니다.
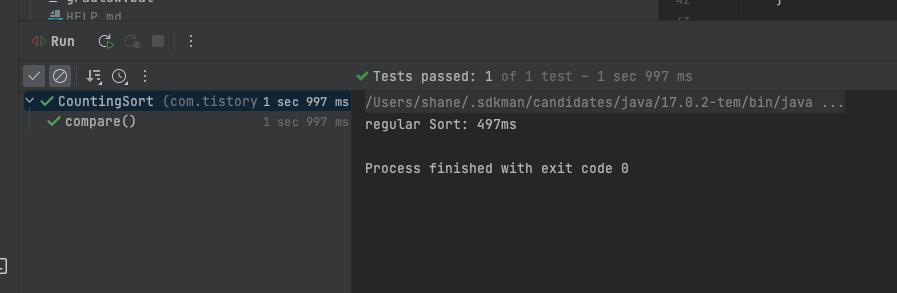
497 ms
지금부터 카운팅 정렬을 활용해 이 문제를 풀어보고, 비교를 해 보겠습니다.
Counting Sort
카운팅정렬은 데이터의 범위가 좁을 때 선형시간내에 정렬을 해 내는 기법입니다.
대개의 경우 자료의 최대값과 최소값이 주어질 때 쉽게 사용할 수 있으며, 주어지지 않았지만 카운팅 정렬이 효율적일 만큼 데이터의 범위가 좁다는 확신이 있는 경우라면 먼저 최대 및 최소값을 찾기 위해 한번 순회를 한 뒤에 사용해도 괜찮습니다.
구현
테스트 코드를 먼저 작성 합니다.
@Test
public void countSortTest() {
int[] data = {1, 5, 5, 4, 4, 3, 3};
Consumer<int[]> countSort = new Consumer() {
@Override
public void accept(Object o) {
// TODO
}
};
countSort.accept(data);
System.out.println(Arrays.toString(data));
assertThat(data).isSorted();
}이제 accept 함수를 채워 주면 됩니다.
MAX 크기의 배열을 만든 뒤에, data 배열을 순회 하며 각 갯수(문제에선 각 사람의 형제 수)에 해당하는 배열의 값을 한개씩 늘려주는 식 으로 직관적으로 구현 해 보았습니다.
그리고 전체 카운팅이 끝나면, 다시 배열의 처음부터 들어갈 숫자를 채워 넣어 줍니다. 코드는 아래와 같습니다.
final int MAX = 14;
@Test
public void countSortTest() {
int[] data = {1, 5, 5, 4, 4, 3, 3};
Consumer<int[]> countSort = arr -> {
int[] counts = new int[MAX];
for (int i : arr) {
counts[i]++;
}
int index = 0;
for (int i = 0; i < counts.length; i++) {
int count = counts[i];
for (int j = 0; j < count; j++) {
arr[index++] = i;
}
}
};
countSort.accept(data);
System.out.println(Arrays.toString(data));
assertThat(data).isSorted();
}테스트
이제 작성한 카운트 정렬 Consumer를 활용 해 비교 해 보겠습니다.
전체 테스트 코드는 아래와 같습니다.
CountingSort.java
package com.tistory.shanepark.sort;
import org.junit.jupiter.api.Test;
import java.util.Arrays;
import java.util.Random;
import java.util.function.Consumer;
import static org.assertj.core.api.Assertions.assertThat;
public class CountingSort {
final int POPULATION = 50_000_000;
final int MAX = 14;
@Test
public void countSortTest() {
int[] data = {1, 5, 5, 4, 4, 3, 3};
CountingSort.accept(data);
System.out.println(Arrays.toString(data));
assertThat(data).isSorted();
}
@Test
public void compare() {
int[] siblings = randomArray();
long start1 = System.currentTimeMillis();
sortSiblings(siblings, (Consumer<int[]>) arr -> Arrays.sort(arr));
System.out.println("regular Sort" + ": " + (System.currentTimeMillis() - start1) + "ms");
siblings = randomArray();
long start2 = System.currentTimeMillis();
sortSiblings(siblings, CountingSort);
System.out.println("CountingSort sort" + ": " + (System.currentTimeMillis() - start2) + "ms");
}
Consumer<int[]> CountingSort = arr -> {
int[] counts = new int[MAX];
for (int i : arr) {
counts[i]++;
}
int index = 0;
for (int i = 0; i < counts.length; i++) {
int count = counts[i];
for (int j = 0; j < count; j++) {
arr[index++] = i;
}
}
};
int[] sortSiblings(int[] siblings, Consumer sorter) {
sorter.accept(siblings);
return siblings;
}
private int[] randomArray() {
int[] arr = new int[POPULATION];
for (int i = 0; i < POPULATION; i++) {
arr[i] = new Random().nextInt(MAX);
}
return arr;
}
}코드를 실행 한 결과를 확인 해 보겠습니다.
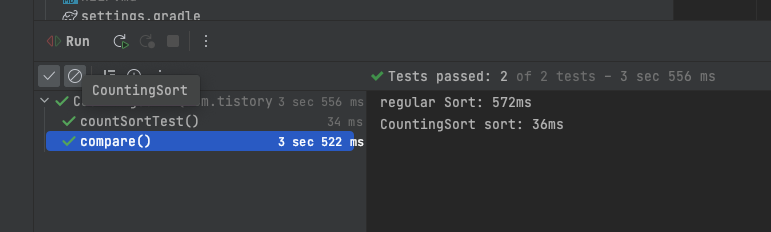
Dual Pivot Sort: 572 ms
Counting sort: 36 ms
엄청난 차이가 있습니다. 사실, Counting Sort는 log(N) 이라기 보다는 log(N+K) 의 시간복잡도에, K는 최대값과 최소값의 차이(현 상황에서는 14) 이지만, 카운팅 정렬이 필요한 상황에서는 보통 K의 값이 워낙에 작기 때문에 거의 무시할 수 있을 정도 입니다.
지금처럼 n 이 50,000,000 까지 커진 상황에서는 단순 계산으로도 nlog(n) 과log(n+k) 은 거의 50,000,000배 나 차이가 납니다. n값이 커질수록 그 차이는 훨씬 벌어집니다.
리팩터링
이번에는 카운팅 정렬을 리팩터링 해 보겠습니다. 지금은 아래와 같이 코드를 작성 해 두었는데요
Consumer<int[]> CountingSort = arr -> {
int[] counts = new int[MAX];
for (int i : arr) {
counts[i]++;
}
int index = 0;
for (int i = 0; i < counts.length; i++) {
int count = counts[i];
for (int j = 0; j < count; j++) {
arr[index++] = i;
}
}
};제 나름대로 이해하긴 쉽게 작성해 보았는데 일반적인 카운팅 정렬과는 조금 차이가 있습니다.
일반적으로는 누적합으로 구현합니다.
Consumer<int[]> CountingSort = arr -> {
int n = arr.length;
int sorted[] = new int[n];
int count[] = new int[MAX];
Arrays.fill(count, 0);
for (int i = 0; i < n; ++i) {
count[arr[i]]++;
}
for (int i = 1; i < MAX; ++i)
count[i] += count[i - 1];
for (int i = n - 1; i >= 0; i--) {
sorted[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}
for (int i = 0; i < n; ++i)
arr[i] = sorted[i];
};
일반적인 구현
전체 코드는 https://github.com/Shane-Park/markdownBlog/blob/39279b797d46df054618ec87dc2d58ad0e2447bb/projects/java/src/main/java/com/tistory/shanepark/sort/CountingSort.java 에서 확인 하실 수 있습니다.
마치며
지금까지 카운팅 정렬에 대해 알아보았습니다. 정렬이 필요한 순간에, 데이터의 범위가 좁다면 카운팅 정렬을 활용한 성능 향상을 고려 해 보세요.
추가로 카운팅 정렬에 대해 연습을 하고 싶다면 LeetCode에 태그된 아래 5개의 문제를 확인 해 보세요. 전체적으로 난이도가 높지 않고 사실 다른 정렬을 사용해도 풀 수 있는 문제지만, 카운팅 정렬을 활용하면 시간 백분위가 제법 좋게 나올 수 있습니다.
https://leetcode.com/tag/counting-sort/
이상입니다.
References
'Development > Problem Solving' 카테고리의 다른 글
| Leetcode) TreeNode.java (0) | 2022.02.20 |
|---|---|
| Leetcode) 소개 및 풀이 코드 Github에 자동 커밋방법 (0) | 2022.01.16 |
| 문제풀이: 가장 긴 팬린드롬(palindrome) (0) | 2021.12.18 |
| JAVA로 알아보는 힙 (Heap) 자료구조 (0) | 2021.10.16 |
| 피보나치 수열과 프로그래머스 땅따먹기 문제로 알아보는 Dynamic Programming (동적 프로그래밍) (0) | 2021.07.31 |